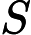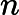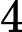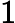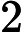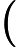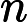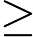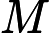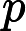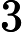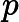リュカ-レーマー・テストの背景を知ったら感動してしまった

こんにちは。ドット会中の人です。

先日，リュカ-レーマー・テストの十分性の証明を読み解く記事を公開しました。

このちょっと後に読んだ本に，このテストの原型となったリュカ・テストがなんと載っており，
これが他の様々な数論的概念と結びついていることを知って，感動してしまったので，
今回はそのことについて，↑の記事の補足として，書こうと思います。

読んだ本が面白かったのでその紹介¶

読んだのは，「大学入試問題で語る数論の世界―素数、完全数からゼータ関数まで」という本です。

この本はめちゃくちゃ面白いです。
他の数論的概念についても書かれていますが，全体的に以下のような数論の面白さを体感することができました。

証明は出来ても想像してみると不思議なことが多い
代数的には取るに足らないことが，数論という観点から見ると急に深くなる
ちょっとした現象なのに，背後に壮大な理論が隠れていることがある
(今回のリュカ・テストのように)全く別の現象が突然出会うことがある

様々な入試問題が体系的に配置されており，スムーズに理解することが出来ました。

リュカ・テスト¶

リュカ-レーマー・テストは，リュカ・テストを改良したものです。リュカ-レーマー・テストの背景を知るためには，リュカ・テストについて知っておく必要があります。ここで簡単に説明します。

リュカ-レーマー・テストは，次のように定義される数列 $S_{n}$ を用いました。↑の記事で述べたとおりです。

S_{0} = 4, S_{n} = S_{n - 1}^{2} - 2 (n \geq 1)

そして，メルセンヌ数(後で説明します)を $M_{n} = 2^{n} - 1$ と定義した時， $p$ を奇素数 $(p \geq 3)$ として， $S_{p - 2}$ が $M_{p}$ で割り切れることと， $M_{p}$ が素数であることが同値であることを用いるのが，このテストでした。

この数列がどうテストで生かされるかは，十分性だけですが，こちらの記事を参照してください。

一方，リュカ・テストは，次のように定義される数列 $s_{n}$ を用います。

s_{1} = 3, s_{n} = s_{n - 1}^{2} - 2 (n \geq 2)

リュカ-レーマー・テストで使われる数列はこの数列 $s_{n}$ の初項を改造したものだと言えますね。
※ん？初項が $n = 0$ か $n = 1$ かで違うって？勘のいいg…

リュカ・テストは，次のような条件で，メルセンヌ素数を判定します。
（出典は先ほど紹介した本です）
$p$ が $4$ で割って $3$ 余る素数のとき，

$s_{1}, s_{2}, s_{3}, \dots, s_{p - 1}$ のどれもが $2^{p} - 1$ で割り切れないならば $2^{p} - 1$ は合成数といえる
$s_{p - 1}$ が $2^{p} - 1$ で割り切れるならば $2^{p} - 1$ は素数といえる

つまり，リュカ-レーマー・テストは，リュカ・テストで使われる数列を改良し，条件を緩め，さらにメルセンヌ素数であることの必要十分条件まで導けるようにしてしまった，ということですね。

リュカ数列との関係¶

さて，リュカ・テストで用いられる数列 $s_{n}$ が，実はリュカ数列と関係があります。
リュカ数列は，基本的にはフィボナッチ数列と同じルールで生み出され，初項が2となるようにした数列でした。
実際の値を並べると，2,1,3,4,7,11,18,29,47,…となります。

リュカ数列 $L_{n}$ の漸化式は，もちろん次のように表されます。

L_{0} = 2, L_{1} = 1, L_{n + 2} = L_{n + 1} + L_{n}

そして，一般項は，2次方程式 $x^{2} - x - 1 = 0$ の2つの解を $α, β (α > β)$ とすると，次のようになります（この2次方程式は黄金比の数を生み出す方程式です）。

L_{n} = α^{n} + β^{n}

余談ですが，黄金比 $ϕ (= α)$ を用いると， $L_{n} = ϕ^{n} + (1 - ϕ)^{n}$ ですね。
もう少し余談をすると，漸化式 $a_{n + 2} = a_{n + 1} + a_{n}$ で表される数列の一般項は， $a_{n} = A α^{n - 1} + B β^{n - 1}$ の形になります。フィボナッチ数列の一般項は， $F_{n} = \frac{α}{\sqrt{5}} \cdot α^{n - 1} + (- \frac{β}{\sqrt{5}}) \cdot β^{n - 1}$ となるようです（すべてこの本に書いてありました）。

さて，リュカ数列の中で $n = 2^{m}$ と表される項だけ取り出してみます。
この数列を $s_{n}^{'}$ とします。

s_{n}^{'} = α^{2^{n}} + β^{2^{n}}

こちらの記事で，リュカ-レーマー・テストの数列 $S_{n}$ は， $α = 2 + \sqrt{3}, β = 2 - \sqrt{3}$ として $S_{n} = α^{2^{n}} + β^{2^{n}}$ となったことから，確かに似ているとわかります。

漸化式を求めてみましょう。
解と係数の関係より， $α β = - 1$ を用いています。 $n \geq 2$ のとき，

s_{n}^{'} = α^{2^{n}} + β^{2^{n}} = (α^{2^{n - 1}} + β^{2^{n - 1}})^{2} - 2 α^{2^{n - 1}} β^{2^{n - 1}} = s_{n - 1}^{' 2} - 2 \cdot (- 1)^{2^{n - 1}} = s_{n - 1}^{' 2} - 2

さらに， $s_{1}^{'} = α^{2} + β^{2} = 3$ なので，

s_{n} = s_{n}^{'}

だと言え，先ほどの数列がリュカ数列から導かれた $s_{n}^{'}$ に等しいことが言えました。

※ネタバラシ：先ほどなぜ初項を $s_{0}$ にしなかったかというと， $s_{0}$ はリュカ数列からは導けないからです。実は， $s_{1}$ と $s_{0}$ の関係性だけ，漸化式が異なります。 $α^{2^{n - 1}} β^{2^{n - 1}}$ の部分ですが， $n = 1$ の時のみ， $2^{n - 1}$ が奇数になるからです。リュカ-レーマー・テストの数列は，リュカ数列から切り離しているのでしょう。 $S_{0}$ を $n \geq 2$ の時の漸化式と同様の関係から導いているように見えます。

リュカ数列という全く関係ないように見える数列が，素数判定法としてメルセンヌ数と不思議なつながりを持っているのは，圧巻です。

メルセンヌ素数の判定法って何がうれしいの？¶

本題はもう終わりました。後はおまけです。
あの本に書いてあったことを，自分なりにまとめてみます。

リュカ・テストやリュカ-レーマー・テストは，メルセンヌ数が素数であるか，つまりメルセンヌ素数であるかを判定するものでした。

なぜメルセンヌ素数をわざわざ「判定」しなければならないのでしょうか。
普通に $M_{n} = 2^{n} - 1$ なのだから，素因数分解できるか調べればよいのではないでしょうか。

そう簡単に素因数分解ってできるものではないですよね。数が大きくなればなるほど，素因数は見つけづらくなります。
例えば，RSA暗号も，大きな数の素因数分解がしづらく， $ϕ (x)$ （オイラーのトーシェント関数；正の整数 $x$ と互いに素である $1$ 以上 $x$ 以下の自然数の個数を返す）がそう簡単に求まらないことを利用したものです。（ここは別の所で知りましたが，なんとこの話もあの本に書いてあったとさ。あの本すげえ）

メルセンヌ数は， $n$ に対して指数関数的に $M_{n}$ が大きくなってしまうため，そう簡単に素数かどうか見分けられないわけです。だから，素因数分解をしなくても素数かどうかを判定できる方法として，これらのテストが用いられています。

どうしてメルセンヌ素数を見つけたいの？¶

ではなぜ，わざわざそんな大きなメルセンヌ素数を見つけたいのでしょうか。
これは色々あると思いますが，完全数の発見につながる，というのが大きいと思います。

偶数の完全数は， $2^{n} - 1$ が素数(=メルセンヌ素数)の時， $2^{n - 1} (2^{n} - 1)$ と表されます。また，そう表される場合に限ります(証明はオイラー)。

つまり，メルセンヌ素数を見つけられれば，完全数の発見につながるわけです。

どうして完全数を見つけたいのでしょうか。
これは周りのいろんな人に聞いたんですが，正直実用的なメリットは分かりませんでした。
完全数の神秘的な面に多くの人が惹かれ，純粋な好奇心から52個目(2021年3月現在)の完全数を見つけようとしているのだとすれば，数学の研究の原動力は実利とは異なる所にあり，美しい世界だな，と思いました。そうなのだと信じたいですが，どうなのでしょう。

まとめ¶

この前の記事では，証明の面白さに着目して説明しましたが，
今回は他の現象との結びつきの面白さについて書いてみました。
2度おいしくていいですね。

完全数―メルセンヌ数―リュカ・テスト―リュカ数列―黄金比，というマップが見えました。全く異質に見える2つの地点の間が，このように結ばれているのは本当に面白いですね。